Teaching a machine to play a rare, difficult game

Inductive reasoning, the process of inferring patterns from an analysis of a set of data, isn't normally taught in schools and is difficult for most people without practice. However, machine learning techniques are known to succeed in datasets with strong patterns.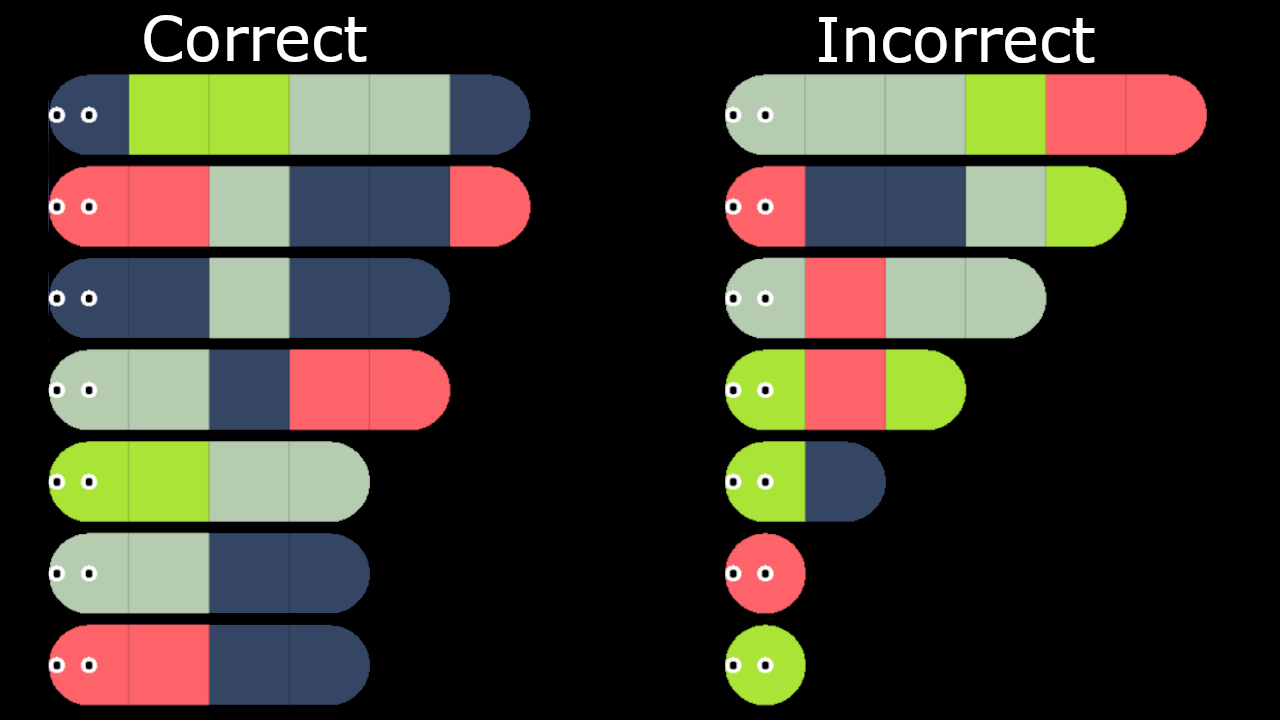

  Ryan Wiesenberg - 16 Jan 2022

Caterpillar Logic is a mobile game with a simple premise:

1. Review the caterpillars generated by the game to find a pattern.
2. Check your hypothesis by creating and checking your own caterpillars.
3. Test of 15 newly generated caterpillars to prove your hypothesis.

The caterpillars are composed of one to seven segments of four possible colors, red, green, blue, and grey and each level starts by presenting you with 14 randomly generated caterpillars, split evenly between correct and incorrect.

Inductive Reasoning

Caterpillar Logic is an example of an inductive reasoning game, which tends to be a rare mechanic. Other examples include:

1. Zendo - puzzle game
2. Eleusis - card game

Typically, we are taught deductive reasoning in our youth, given a rule or pattern we have learned the ability to determine if a data point matches the rule or breaks it.

Scientists and researchers learn how to do the inverse within their field. They form a hypothesis based on an observed pattern and then gather more information to either prove or disprove their guess. This process is called inductive reasoning.

I was introduced to this game by my friend Max Merlin, who has been entertaining the idea of different algorithmic ways to solve it. I proposed that machine learning, which is known for excelling in areas of high pattern, could be a viable candidate for solving this system.

So, as all machine learning evaluations start, I set off to collect my dataset.

Data Collection

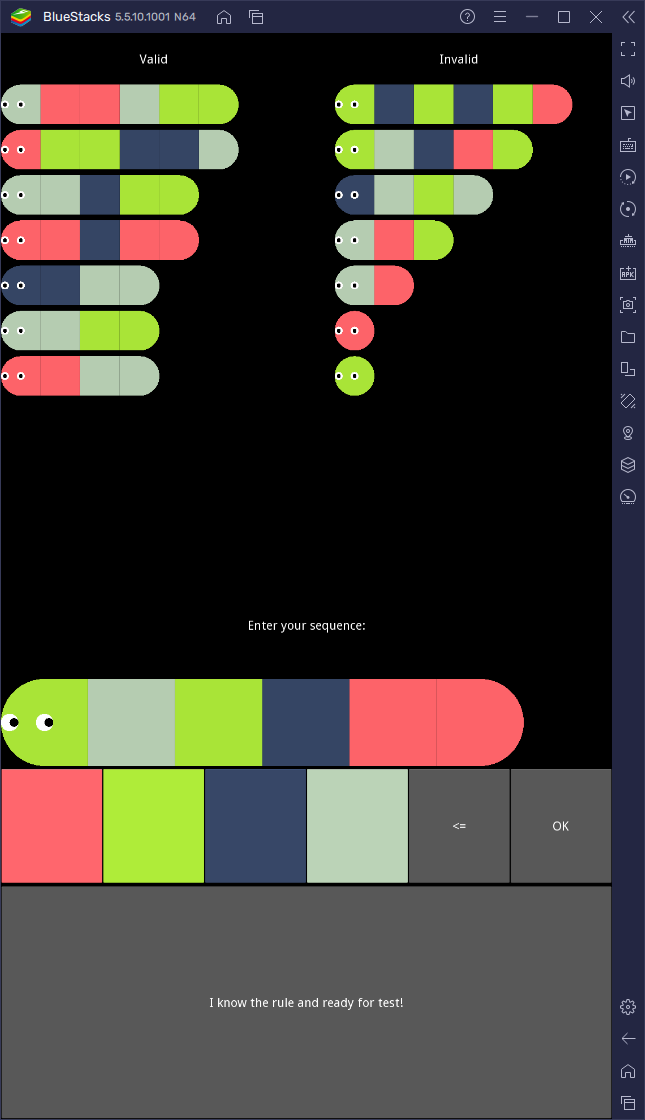
The search space for Caterpillar logic is fairly limited with only four colors and a maximum of seven segments.

However, the game itself only presents caterpillars of up to length 6:

To best estimate the experience of a player, I did not include any assumptions about the data in the collection process other than the search space itself.

First Attempt: Input Farming

My first thought was to use the sequence checking function of the game to test randomly chosen sequences from the list of all possible caterpillars:

1. Generate the full search space: 21871 caterpillars
2. Choose a subset randomly: 400 caterpillars (~1%)
3. Check if each caterpillar is valid or invalid and record

Additionally, because the space for single length caterpillars is so small I made sure each of the four possible caterpillars was included in the dataset.

I designed a tool to poll the colors and press the buttons itself. However, I still encountered two problems:

1. Randomly choosing caterpillars does not guarantee any valid caterpillars.
2. The mobile game slowed down after the first hundred entries, likely due to a garbage collection issue.

To be fair to the developer, this use-case was extremely unlikely and definitely outside the scope of a typical mobile user.

Working Method: Level Refresh

The method that I ended up using was simply repeatedly opening and closing the page to have the game refresh the caterpillars for me:

1. Generate the system-limited search space: 5487 caterpillars
2. Refresh the page until sufficient collected: 274 caterpillars (5%)
3. Store all valid and invalid caterpillars

This eliminated both of the problems from the method above, but I am concerned this method may result in capturing all possible valid caterpillars, especially in tight pattern spaces.

Training and Results

After some experimenting, I decided on a network with 5 linear layers and a final binary classifier:

1. ReLU(Linear 7->32)
2. ReLU(Linear 32->32)
3. Dropout(p=0.1)
4. ReLU(Linear 32->64)
5. ReLU(Linear 64->16)
6. Dropout(p=0.1)
7. ReLU(Linear 16->1)

Here is an example training run:

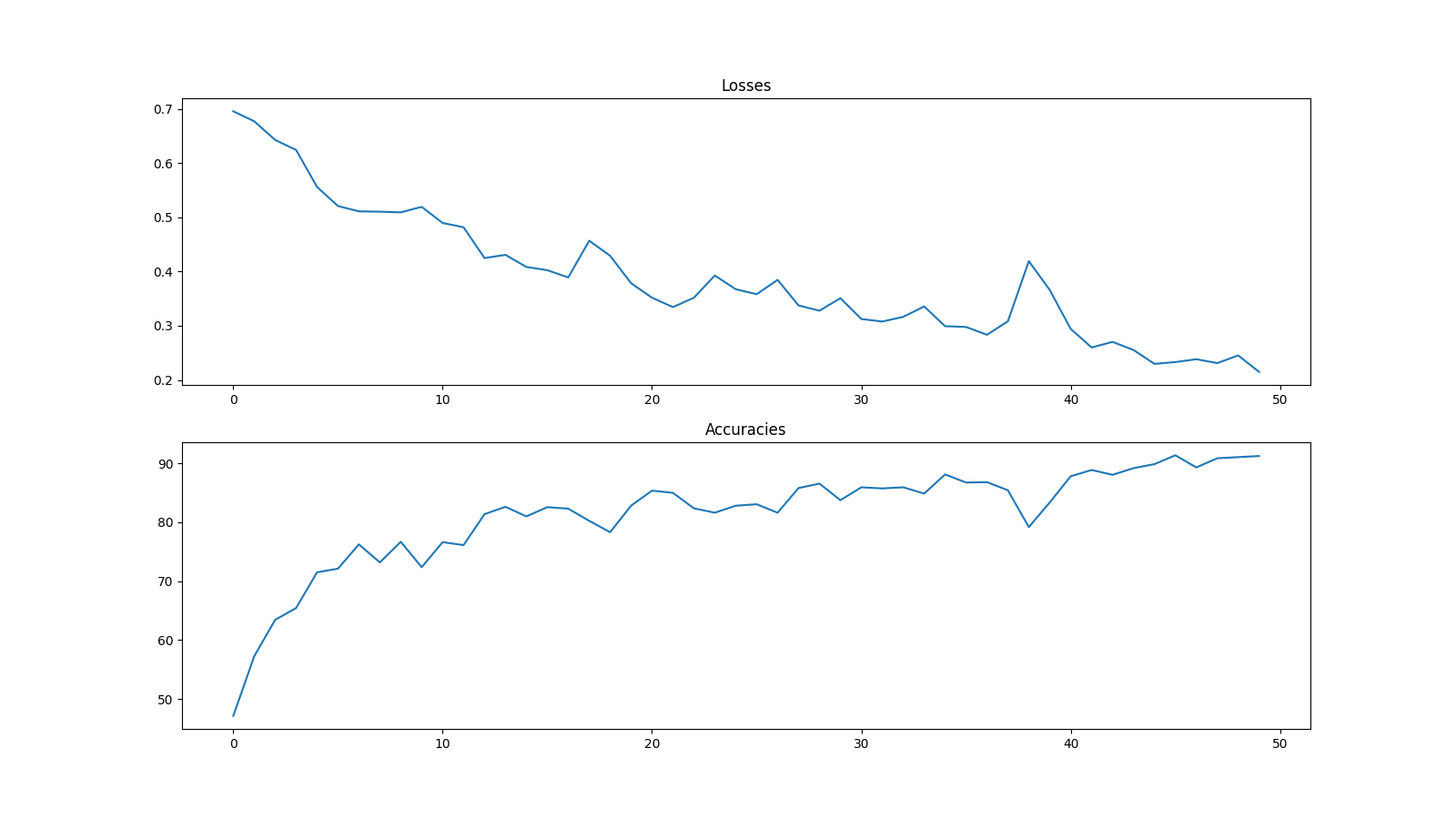
As you can see, the network is improving over time but the results are inconsistent on the validation data, with varying levels of success, but always better than 70% regardless of level chosen. This at least proves the network is learning, but the space may be too small for full success for this network type.

After a few attempts (5… oof) on a random level the network successfully guessed 15/15 test caterpillars!

We have a winner!

Conclusion

There is some proof that a machine learning approach could solve an inductive reasoning game, Caterpillar Logic. However, I am concerned that the method I used with the level refresh could incidentally learn all possible valid caterpillars for some of the more difficult levels.

If I to revisit this problem, I would try two other methods of learning:

1. To compare the algorithm’s performance more easily with that of a human player: A pseudo genetic algorithm that would first learn the presented valid and invalid and then try caterpillars itself until it was confident enough in the test.
2. To improve the networks result: Develop a form of recurrent neural network (RNN) that can use the sequential nature of the caterpillars to better inform itself.

Feel free to reach out with any feedback or collaboration requests!
View code used in this post